Consideriamo adesso nuovamente un semplice circuito costituito da una resistenza e da un condensatore collegati in serie. Supponiamo inoltre che ai capi di tale serie venga applicata dall’esterno una tensione vin(t), variabile nel tempo. Supponiamo di essere interessati a determinare l’andamento nel tempo della tensione vc(t) sul condensatore:
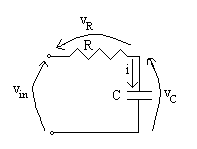
L’analisi del circuito procede dunque anzitutto ricavando le formule (i modelli matematici) che descrivono i due componenti. Per quanto riguarda il resistore il modello matematico è rappresentato dalla legge di Ohm:
vR(t) = R . i(t)
Si osservi come tale equazione sia stata scritta usando per la tensione e la corrente gli stessi nomi riportati sullo schema circuitale. Per quanto riguarda il condensatore, la formula è quella ricavata in una precedente lezione:
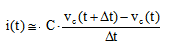
Osserviamo inoltre che le tensioni vR(t) e vc(t) sono legate fra loro dalla legge di Kirchhoff alla maglia nel circuito:
vin(t) = vR(t) + vc(t)
Per risolvere il sistema di equazioni possiamo dunque partire dalla precedente equazione e sostituire in essa al posto di vR(t) l'espressione ricavata dalla legge di Ohm del resistore:
vin(t) = R . i(t) + vc(t)
A questo punto è possibile eliminare i(t), usando il modello matematico del condensatore:
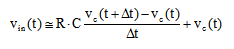
Riscriviamo infine la formula così trovata con alcuni passaggi matematici:
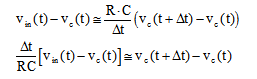
da cui infine:
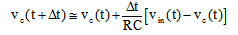
La formula così trovata costituisce il modello iterativo del circuito RC serie. Essa consente cioè il calcolo della tensione sul condensatore vc in ogni istante di tempo e tale calcolo viene effettuato ripetendo (cioè iterando) la formula stessa.
Supponiamo ad esempio che si abbia R = 10 kΩ e C = 2 µF e supponiamo che la tensione di ingresso vin sia costante e pari a +5V. Per effettuare il calcolo dobbiamo conoscere anche il valore di vc all’istante zero iniziale: supponendo il condensatore inizialmente scarico, abbiamo vc(0) = 0 V.
Il valore di Δt invece non è un parametro (cioè un dato) del circuito, ma da esso dipende sostanzialmente la precisione del calcolo. In generale, più Δt è piccolo, più i valori calcolati saranno precisi. Tuttavia, riducendo Δt, aumenta il numero di calcoli necessario e dunque in generale la scelta di Δt sarà frutto di un compromesso fra precisione e velocità di calcolo. Come semplice regola generale conviene scegliere un valore di Δt più piccolo della costante di tempo τ = R.C del circuito.
Supponiamo per esempio di scegliere, piuttosto arbitrariamente, Δt = 1ms. Il calcolo procede partendo dal valore iniziale vc(0) = 0 V e calcolando quindi la tensione vc(t) all'istante di tempo successivo t+Δt = 0 + 1ms = 1ms nel seguente modo:
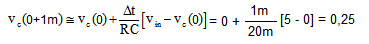
A questo punto il nuovo valore appena calcolato vc(1m) = 0,25 V può essere utilizzato per calcolare il valore all'istante di tempo successivo t+Δt = 1ms + 1ms = 2ms nel seguente modo:
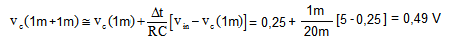
Il procedimento può essere ripetuto (da qui il nome modello iterativo) per tutti gli istanti di tempo successivi per calcolare allo stesso modo l'andamento nel tempo della tensione sul condensatore. La tabella seguente mostra i risultati del calcolo effettuato con valori diversi di Δt (i risultati più precisi sono quelli sull'ultima colonna, con Δt più piccolo):
|
t
[secondi] |
vc
con
Dt =0,01s |
vc
con
Dt = 1 ms |
vc
con
Dt =0,1ms |
|
0,0000 |
0,0000 |
0,000 |
0,000 |
|
0,0001 |
|
|
0,025 |
|
0,0002 |
|
|
0,050 |
|
0,0010 |
|
0,250 |
0,244 |
|
0,0020 |
|
0,490 |
0,477 |
|
0,0100 |
2,500 |
2,006 |
1,971 |
|
0,0200 |
3,750 |
3,208 |
3,165 |
|
0,1000 |
4,995 |
4,970 |
4,967 |
|
0,2000 |
5,000 |
5,000 |
5,000 |
Il grafico seguente mostra l'andamento della tensione sul condensatore così calcolata:
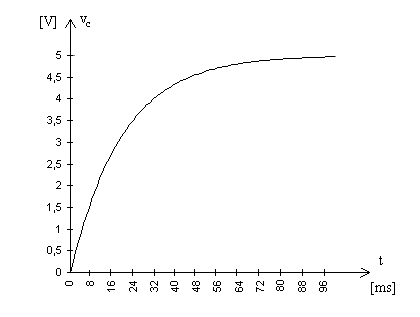
Riconosciamo facilmente il tipico andamento della carica di un condensatore.
Sito realizzato in base al template offerto da
http://www.graphixmania.it