Per ragioni che saranno più chiare nel seguito, i numeri all'interno dei dispositivi digitali non sono rappresentati nella forma usuale a cui siamo abituati. La numerazione che noi usiamo di solito viene detta decimale in quanto si basa sull'uso delle dieci cifre da 0 a 9. La scelta della base 10 non ha nessuna particolare motivazione pratica: deriva dal fatto che abbiamo dieci dita nelle mani per contare. Presso vari popoli sono presenti altri sistemi di numerazione in base 5 e in base 20, anche questi basati sul numero di dita (di una sola mano o di mani e piedi insieme). D'altra parte anche noi usiamo(a volte inconsapevolmente) altre basi numeriche, come per esempio la base sessanta (sessagesimale) utilizzata per le misure di tempo e angolari.
La rappresentazione di un numero decimale utilizza una notazione posizionale, in quanto la posizione di una cifra all'interno di un numero ne stabilisce il valore. Così per esempio nel numero 5605 il primo cinque vale 5000 mentre l'ultimo vale solo 5: il valore è determinato dalla posizione della cifra; le cifre più a sinistra pesano di più di quelle più a destra. Ogni cifra pesa 10 volte di più di quella immediatamente precedente (si tratta di un sistema di numerazione detto appunto in base 10).
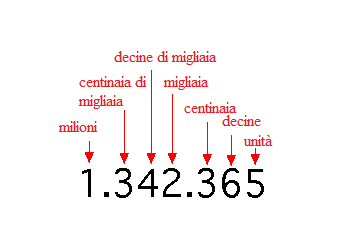
La notazione posizionale fu una grande invenzione (probabilmente fu inventato in India e arrivò in Europa attraverso gli arabi) perché semplificò grandemente i calcoli, rispetto ai precedenti numeri romani.
Il sistema binario, usato dai computer e da tutti i dispositivi digitali, utilizza invece solo due cifre 0 e 1. Le cifre binarie vengono dette bit (contrazione di binary digit che in inglese significa appunto cifra binaria).
Anche in questo caso si tratta di un sistema posizionale, solo che il peso di ogni cifra varia secondo le potenze crescenti di 2 (sistema in base 2). La figura seguente mostra per esempio il numero 45 rappresentato in binario:
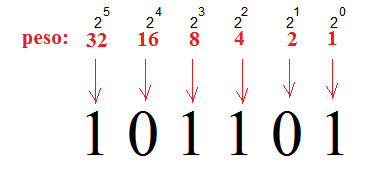
Il primo bit (quello più a sinistra) di ogni numero binario viene detto bit più significativo (Most Significant Bit o MSB), mentre il bit più a destra viene detto bit meno significativo (Least Significant Bit o LSB).
Possiamo usare la notazione posizionale per interpretare un numero scritto in una base qualsiasi, anche diversa da 10.
Consideriamo per esempio il numero (243)5 cioè 243 in base 5. Esso può essere scomposto nel seguente modo:
2 x 52 + 4 x 51 + 3 x 50 = 2 x 25 + 4 x 5 + 3 x 1 = (73)10
In altre parole 243 in base 5 equivale a 73 scritto in base 10.
Sito realizzato in base al template offerto da
http://www.graphixmania.it