Nell'elettronica digitale si chiama circuito combinatorio (o rete combinatoria) un circuito logico in cui le uscite sono funzione unicamente degli ingressi allo stesso istante di tempo. Per tale motivo sono anche chiamati circuiti senza memoria (distinguendosi in questo dai circuiti sequenziali, di cui parleremo più avanti, che invece possiedono memoria).

In pratica sono combinatori tutti i circuiti digitali visti finora, cioè le porte logiche e i circuiti ottenuti combinando fra loro porte logiche. Tutti i circuiti il cui funzionamento può essere rappresentato da un'espressione logica sono circuiti combinatori.

Addizionatore completo (full adder) a due bit

Uno dei circuiti combinatori più interessanti è l'addizionatore completo (full adder) , mediante il quale è possibile realizzare elettronicamente la somma di due numeri binari. Per la spiegazione della somma binaria si rimanda alla precedente lezione. Come abbiamo visto là, se si usa il complemento a 2 per rappresentare i numeri negativi, lo stesso circuito può effettuare somme o sottrazioni, senza alcuna differenza.

Concentriamoci inizialmente sul problema di progettare un addizionatore a una sola cifra. Tale circuito dovrà sommare fra loro i bit A e B corrispondenti ai due numeri binari e l'eventuale riporto dalla cifra precedente (C_i, il riporto si indica di solito con C perché in inglese si chiama carry). L'addizionatore si chiama completo proprio perché considera anche la somma dell'eventuale riporto (mentre l'addizionatore senza riporto viene detto half adder).

In uscita l'addizionatore deve produrre un bit di somma S e un riporto in uscita C_o. La tabella di verità seguente dovrebbe chiarire il funzionamento del circuito:

A	B	Ci	S	Co
0	0	0	0	0
0	0	1	1	0
0	1	0	1	0
0	1	1	0	1
1	0	0	1	0
1	0	1	0	1
1	1	0	0	1
1	1	1	1	1

Si tratta di una tabella di verità con due uscite che, come abbiamo già visto, corrisponde a due differenti espressioni logiche: una per l'uscita S e l'altra per l'uscita C_o.

Procediamo quindi alla sintesi delle due uscite con il metodo della forma canonica somma dei prodotti e procedendo quindi a semplificazioni successive:

S = A^.B^.C_i + A^.B^.C_i + A^.B^.C_i  + A^.B^.C_i = C_i^.(A^.B+A^.B) + C_i^.(A^.B+A^.B) =

= C_i^.(AB)+ C_i^.(AB) = C_i^.(AB)

C_o = A^.B^.C_i +A^.B^.C_i +A^.B^.C_i  +A^.B^.C_i = C_i^.(A^.B + A^.B) + A^.B^.(C_i +C_i) = C_i^.(AB) + A^.B

Le semplificazioni precedenti possono forse sembrare poco intuitive, ma sono mirate a realizzare l'addizionatore col numero minore di porte logiche possibile. Il risultato finale è mostrato nella figura seguente:

Somma di numeri binari a più cifre

Collegando fra loro in cascata (cioè con le uscite dell'uno collegate con gli ingressi dell'altro) più addizionatori a una sola cifra, è possibile realizzare un addizionatore binario a più cifre.

Schematizziamo intanto un singolo addizionatore (realizzato come visto sopra) come un blocco avente tre ingressi A₀, B₀ e C₀ e due uscite S₀ e C₁. I pedici 0 e 1 si riferiscono alla posizione della cifra all'interno del numero binario (come sarà più chiaro nel seguito):

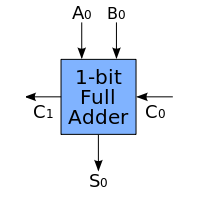
A questo punto è possibile realizzare un addizionatore a 4 bit collegando fra loro 4 blocchi come il precedente in questo modo:

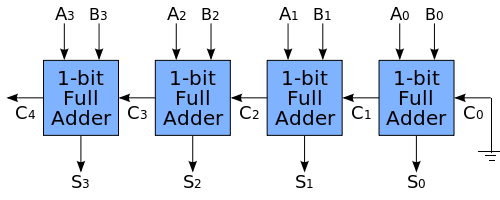
Si noti che il riporto C₀ in ingresso al primo full adder (quello che deve sommare i due bit meno significativi del numero binario) è collegato a massa in modo da fornire in ingresso un valore binario zero (fisso). 

Full adder integrati

I full adder sono anche disponibili sotto forma di circuito integrato. La figura seguente mostra come esempio la piedinatura di un 4008, full adder integrato a 4 bit della famiglia logica CMOS:

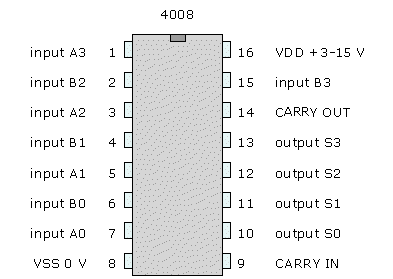
I piedini A0... A3 e B0... B3 servono per inserire le cifre binarie dei due nummeri da sommare (la cifra 0 è quella meno significativa). I piedini di uscita S0 e S3 forniscono i bit della somma. Il piedino CARRY IN serve per un eventuale riporto in ingresso, mentre CARRY OUT serve per segnalare un eventuale riporto in uscita: questi due piedini sono molto utili per collegare in cascata due o più integrati 4008 in modo da realizzare facilmente un sommatore a 8 (o più) bit.

La figura seguente mostra la possibile realizzazione di un addizionatore a 8 bit:

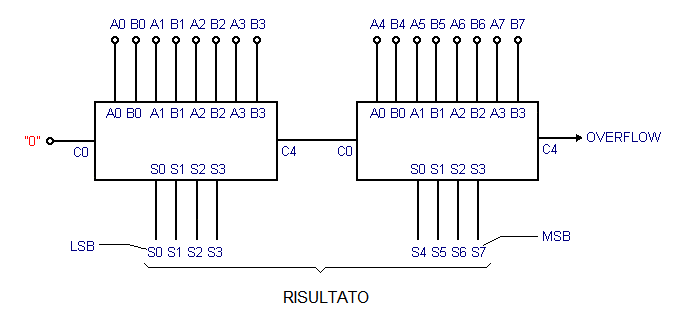
Si osservi come l'eventuale riporto dall'ultima cifra del secondo addizionatore venga usato per segnalare una condizione di overflow (letteralmente di straripamento): quando c'è un riporto sulla somma delle due cifre più significative del numero significa infatti che il risultato non può essere rappresentato con solo otto cifre.

precedente - successiva

Sito realizzato in base al template offerto da

http://www.graphixmania.it

Segui @ElePrograMania