Un tono puro è un'onda sonora perfettamente sinusoidale e dunque interamente caratterizzabile da tre parametri:
- l'ampiezza, cioè il valore massimo dell'onda (a sua volta legato alla potenza sonora dell'onda stessa);
- la frequenza, cioè il numero di oscillazioni al secondo dell'onda;
- la lunghezza d'onda, cioè la distanza nello spazio fra due creste successive (legato alla velocità di propagazione dell'onda nel mezzo tramissivo).
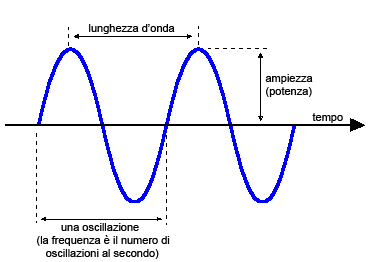
Dal punto di vista della percezione umana, i due parametri fondamentali sono l'ampiezza e la frequenza del tono puro.
Ampiezza e volume
L'ampiezza di un tono puro sinusoidale viene percepito dall'orecchio come volume o intensità sonora. Maggiore è l'ampiezza dell'onda, maggiore sarà il volume sonoro percepito.
Si definisce soglia di udibilità la minima intensità sonora che l'orecchio umano è in grado di percepire. L'esperienza mostra che tale soglia varia da individuo a individuo (per esempio si innalza all'aumentare dell'età del soggetto), e, soprattutto che, anche per un singolo individuo, essa dipende dalla frequenza del suono ascoltato.
Il livello di intensità sonora si misura in decibel di pressione sonora (dBSPL o pi¨ brevemente dB). L'intensità sonora IdB è definta come
IdB= 10 log10 (I/I0)
dove I0 è un valore convenzionale, ottenuto mediando la soglia di udibilità di molti individui per un suono puro di frequenza di 1000 Hz. Esso vale
I0 = 10-12 W/m2
Il rapporto I/I0 Ŕ un numero puro e la misura in dB rappresenta quanto l'intensitÓ sonora risulta maggiore rispetto alla soglia di udibilitÓ. La tabella seguente riporta l'intensitÓ sonora associata a diversi eventi:
| dBSPL | Sorgente | Numero di volte rispetto all'udibilitÓ |
|---|---|---|
| 300 | Eruzione del Krakatoa nel 1883 | 1030 |
| 250 | All'interno di un tornado | 1025 |
| 180 | Razzo al decollo | 1018 |
| 140 | Colpo di pistola a 1 m | 1014 |
| 130 | Soglia del dolore | 1013 |
| 125 | Aereo al decollo a 50 m | 1012,5 |
| 120 | Sirena, Auto di Formula 1 in pista | 1012 |
| 110 | Motosega a 1 m | 1011 |
| 100 | Discoteca, concerto rock | 1010 |
| 90 | Urlo, fischietto | 109 |
| 80 | Camion pesante a 1 m | 108 |
| 70 | Aspirapolvere a 1 m; radio ad alto volume | 107 |
| 60 | Ufficio rumoroso, radio, conversazione | 106 |
| 50 | Ambiente domestico; teatro a 10 m | 105 |
| 40 | Quartiere abitato, di notte | 104 |
| 30 | Sussurri a 1 m | 1000 |
| 20 | Respiro umano | 100 |
| 0 | Soglia dell'udibile | 1 |
| -9 | Camera anecoica | 0,13 |
Osserviamo che i dB forniscono una scala logaritmica per la misura dell'intensitÓ sonora: ad ogni aumento di 10 dB corrisponde un aumento di un fattore 10 dell'intensitÓ del suono.
L'adozione di tale scala trova giustificazione nel fatto che l'orecchio umano non presenta una sensibilitÓ lineare rispetto all'intensitÓ sonora, ma, in prima approssimazione, la sensibilitÓ cresce in modo logaritmico rispetto all'intensitÓ (cioŔ secondo la scala in dB).
Decibel sonori e decibel di amplificazione
In fisica e in ingegneria spesso si assume, senza neppure esplicitarlo, che i rapporti in dB che verranno calcolati siano sempre relativi a energie o potenze. Questo introduce nei calcoli un fattore 20 che pu˛ creare confusione.
Ad esempio, in elettronica ed elettrotecnica, parlando di rapporti in dB fra tensioni o correnti elettriche, talvolta non si intende il rapporto fra le grandezze stesse, ma fra le potenze che le tensioni svilupperebbero se applicate a una medesima impedenza. Essendo la potenza W proporzionale al quadrato della tensione V, sfruttando le proprietÓ dei logaritmi si ricava la formula seguente:
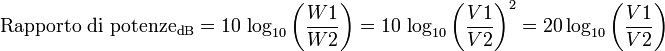
Tale formula vale per˛, solo nell'ipotesi che le tensioni o correnti di ingresso e di uscita vengano applicate a una medesima impedenza: cosa spesso vera per gli amplificatori a radiofrequenza, ma ben lontana dalla realtÓ nella maggior parte dei comuni amplificatori audio.
Frequenza e altezza
La frequenza di un tono puro viene percepito come altezza della nota: note di diversa altezza corrispondono a toni con frequenza diversa. In pratica il termine altezza usato in musica corrisponde alla frequenza misurata della nota.
Ad esempio, la frequenza corrispondente alla nota LA posta al centro della tastiera del pianoforte è pari a 440 Hz. La figura seguente mostra la frequenza corrispondente ad alcune note sul pentagramma musicale:

I valori esatti sono i seguenti:
|
Do 4 |
261,6 Hz |
|
Do # = Re b |
277,2 Hz |
|
Re |
293,7 Hz |
|
Re # |
311,1 Hz |
|
Mi |
329,6 Hz |
|
Fa |
349,2 Hz |
|
Fa # |
370,0 Hz |
|
Sol |
392 Hz |
|
Sol # |
415,3 Hz |
|
La |
440 Hz |
|
La # |
466,2 Hz |
|
Si |
493,9 Hz |
|
Do 5 |
523,3 Hz |
Notiamo che al crescere della frequenza i suoni divengono sempre più acuti. Dunque l'altezza (= frequenza) è una caratteristica del suono che consente di ordinare i suoni in una scala da gravi (o bassi) ad acuti (o alti).
Inoltre fra due note uguali appartenenti a due ottave successive (es. DO 4 d DO 5) la frequenza raddoppia: dunque il concetto musicali di ottava corrisponde a un raddoppio in frequenza.
La figura qui sotto mostra toni puri di altezza (cioè di frequenza) diverse ma con la stessa ampiezza:
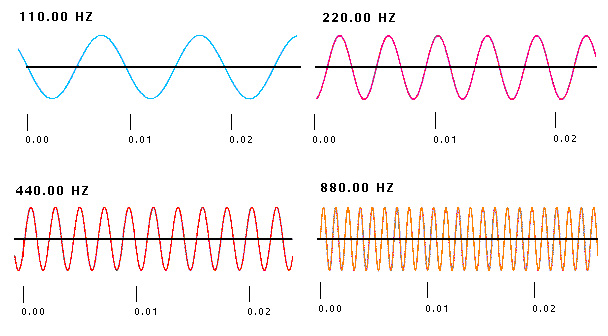
Si dice intervallo o campo di udibilità dell'orecchio, l'intervallo di frequenze che l'orecchio umano è in grado di udire. Tale intervallo varia notevolmente da un individuo all'altro e in base all'età, ma in linea di massima è compreso fra una frequenza minima udibile di 20 Hz e una frequenza massima udibile intorno ai 20 kHz. Al di sotto della minima frequenza si entra nel campo degli infrasuoni e al di sopra della massima si entra nel campo degli ultrasuoni.
Per misurare la risposta in frequenza dell'orecchio si fa uso di uno strumento detto audiometro. In pratica al soggetto vengono fatti ascoltare una serie di suoni con diversa frequenza. In corrispondenza di ogni suono la persona deve regolare l'intensità del suono prodotto in modo da sentirlo sempre come se avesse la stessa ampiezza. Si ottiene in tale modo una curva di questo tipo (detta audiogramma):
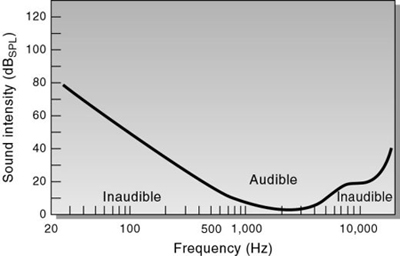
Si osservi che per i suoni a frequenza più bassa e più alta, l'intensità assoluta del suono dev'essere aumentata per mantenere costante l'intensità percepita: ciò è dovuto appunto alla perdita di sensibilità dell'orecchio umano alle basse e alle alte frequenze (il massimo di sensibilità si ha intorno a circa 1000 Hz).
La curva di sensibilità dell'orecchio varia molto fra diverse specie animali, come mostra il seguente audiogramma:
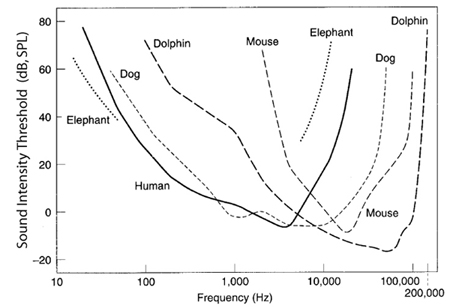
Lunghezza d'onda
Noto l'intervallo delle frequenze udibili possiamo calcolare la lunghezza d'onda dei suoni corripondenti. Assumendo una velocità v del suono in aria pari a 340 m/s, usando la formula
v = λ f
e sostituendo alla frequenza f il limite inferiore (20 Hz) e superiore (20000 Hz) otteniamo, per le onde sonore, lunghezze d'onda comprese tra circa 1,7 cm (suoni acutissimi, ad alta frequenza) e 17 metri (suoni gravissimi, a bassissima frequenza).
Questo dato è molto importante perché fornisce un criterio relativo alla capacità dell'onda sonora di aggirare gli ostacoli (ad esempio la nostra testa, o una colonna, un edificio, una montagna). Il criterio é il seguente: se le dimensioni dell'ostacolo sono minori o paragonabili alla lunghezza d'onda del suono, l'ostacolo non é in genere in grado di fermare il suono che lo investe.
Inoltre la lunghezza d'onda λ fornisce un criterio di percepibilità dell'altezza di un suono in relazione alla dimensione degli ambienti in cui il suono viene prodotto. In pratica il suono viene percepito correttamente se le dimensioni dell'ambiente sono molto maggiori della sua lunghezza d'onda (cioè per ascoltare correttamente suoni molto bassi occorrono ambienti di grandi dimensioni).
Sito realizzato in base al template offerto da
http://www.graphixmania.it