L'enunciato del teorema di Fourier può essere scritto matematicamente mediante una formula detta serie di Fourier:
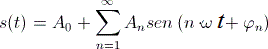
dove:
- s(t) è un generico segnale periodico;
- il simbolo
viene detto sommatoria e serve per indicare una somma di
termini con diversi valori di n; nel nostro caso n varia da 1 fino a
infinito (si tratta dunque di una somma di infiniti termini, detta appunto
serie);
- ω è la pulsazione del segnale periodico s(t) che si vuole scomporre in serie di Fourier;
- A0 rappresenta un'eventuale termine costante o offset (nel caso in cui s(t) fosse un segnale a valore medio non nullo);
- An e φn sono rispettivamente l'ampiezza e la fase della generica armonica n-esima e si dicono coefficienti della serie di Fourier.
Facciamo un esempio. Consideriamo il segnale periodico detto a dente di sega (saw tooth) mostrato in figura:
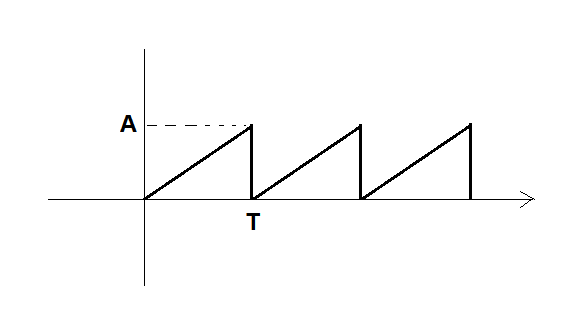
dove A è l'ampiezza e T è il periodo dell'onda. Si può dimostrare che la serie di Fourier corrispondente è la seguente:
Si noti che il primo termine A/2 rappresenta il valore medio (non nullo) del segnale a dente di sega. Inoltre i segni dei diversi termini sono alternati (uno positivo e l'altro negativo), mentre le fasi sono sempre zero per tutti i termini. La serie di Fourier dell'onda a dente di sega può essere sintetizzata nel seguente modo:
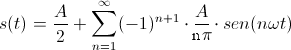
Il fattore (-1)n+1 serve solo per alternare i segni delle armoniche (la prima armonica con n=1 risulta positiva, la seconda con n=2 negativa e così via...).
Un altro modo per esprimere la serie di Fourier dello stesso segnale consiste nel considerare positive le ampiezze di tutte le armoniche e aggiungere una fase ±π alle armoniche pari (equivale a invertirne il segno).
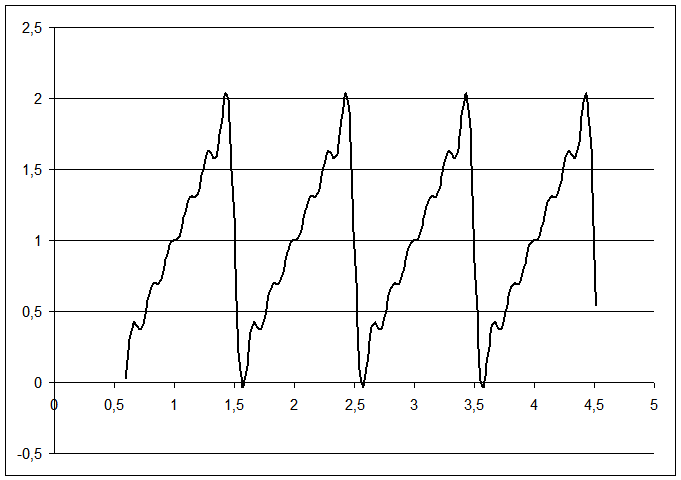
La figura seguente mostra il risultato della somma delle prime 6 armoniche per un'onda con periodo 1 secondo e ampiezza 2:
Sito realizzato in base al template offerto da
http://www.graphixmania.it
