Consideriamo lo schema del derivatore invertente con operazionale:
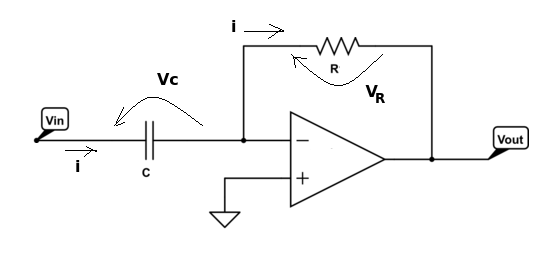
La relazione fra uscita è ingresso è la seguente:
Vout = - RC V'in
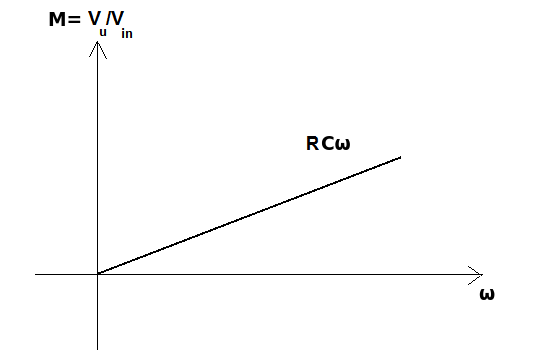
Come si può facilmente osservare, la presenza della derivata rende la risposta in frequenza di questo circuito analoga a quella ricavata per il condensatore. Il grafico del modulo è il seguente (quello della fase è identico a quello visto per il condensatore):
Consideriamo ora l'integratore invertente con operazionale:
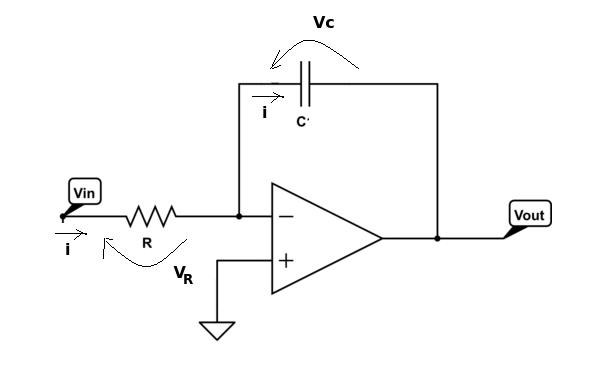
La relazione fra tensione di uscita e tensione di ingresso è:
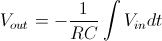
Consideriamo come al solito una tensione di ingresso sinusoidale:
Vin(t) = A sen(ω.t)
Calcolando l'integrale abbiamo dunque:
![]()
Notiamo che il modulo, cioè il rapporto fra le ampiezze della sinusoide di ingresso e di uscita, è dato da:
![]()
Il grafico del modulo in scala lineare è dunque un ramo di iperbole:
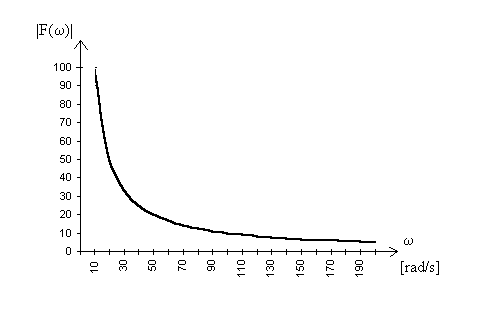
Per quanto riguarda la fase, il grafico è una retta costante di valore +π/2 rad.
Sito realizzato in base al template offerto da
http://www.graphixmania.it