Dal punto di vista matematico una generica sinusoide s(t) può essere rappresentata per mezzo della seguente espressione:
s(t) = A sen(ω.t)
dove "sen" è l'abbreviazione comunemente usata per indicare la funzione "seno", A è l'ampiezza del segnale sinusoidale, ω è la pulsazione della sinusoide, misurata in rad/s.
Il radiante (rad) è l'unità di misura degli angoli piani nel Sistema Internazionale. Un radiante (1 rad) viene definito come quell'angolo al centro di una circonferenza che sottende un arco di circonferenza di lunghezza uguale al raggio. In pratica per ottenere il valore in radianti di un angolo basta dividere l'arco di circonferenza sotteso all'angolo per il raggio della circonferenza stessa: essendo il rapporto fra due lunghezze dunque il radiante non ha dimensioni fisiche.
La funzione seno è una funzione periodica, cioè tale che i suoi valori si ripetono identici ad intervalli di tempo pari a un periodo T. Fra periodo T (misurato in secondi), pulsazione ω (misurata in radianti al secondo) e frequenza f (misurata in hertz), esistono le seguenti relazioni:
ω = 2πf ω=2π/T T=1/f T=2π/ω f=1/T f=ω/(2π)
In pratica la pulsazione e la frequenza misurano la stessa grandezza fisica, ma con unità di misura differenti (rad/s per la pulsazione e Herz per la frequenza). Nel seguito quindi i due termini, pulsazione e frequenza, saranno spesso usati in modo quasi indifferente, per indicare la rapidità con cui il segnale sinusoidale oscilla nel tempo.
Il grafico dell'andamento nel tempo di una generica sinusoide s(t) è mostrato in figura:
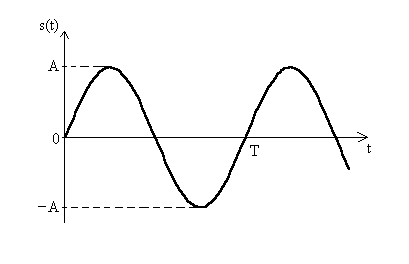
Il lettore probabilmente conosce l'esistenza di una seconda funzione sinusoidale, detta coseno, la cui espressione analitica è
s2(t) = A cos(ω.t)
Dal punto di vista geometrico s2(t) rappresenta, istante per istante, il valore della proiezione sull'asse x del vettore ruotante (fasore). Il grafico della funzione coseno è il seguente:
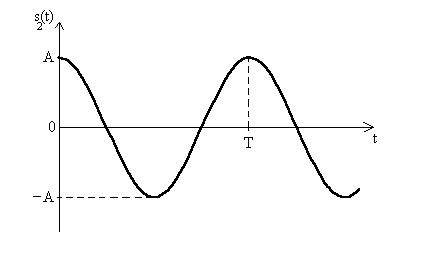
E' interessante osservare che in realtà i grafici di seno e di coseno sono indistinguibili l'uno dall'altro e che pertanto si tratta in pratica della stessa funzione. Infatti, confrontando fra loro i grafici di seno e coseno, notiamo che la forma d'onda dei due segnali è esattamente identica. L'unica differenza è data dalla posizione della curva rispetto agli assi cartesiani (o, più precisamente, rispetto all'origine dei tempi t = 0): infatti la funzione "seno" nell'origine passa per lo zero crescendo, mentre la funzione "coseno" in t = 0 raggiunge il suo valore massimo. Tuttavia il riferimento di tempo t = 0 è arbitrario e dunque la distinzione fra seno e coseno è puramente convenzionale.
Sito realizzato in base al template offerto da
http://www.graphixmania.it