Si definisce capacità del canale la massima velocità di trasmissione teoricamente raggiungibile su un dato canale. Per un canale privo di rumore il primo teorema di Nyquist afferma che la capacità massima teorica di un canale è pari al doppio della sua banda. In formule:

C^binaria_max = 2 B

dove C^binaria_max è la capacità massima misurata in bit/s e B è la banda del canale espressa in Hertz. Per esempio su un canale con banda B = 4 kHz è possibile trasmettere fino a un massimo di 8 kb/s.

Tale risultato deriva dal fatto che, su un canale con banda B, la massima frequenza di segnale che può "passare" è ovviamente uguale a B. Considerando di applicare in ingresso al canale un segnale digitale binario con velocità 2B bit/s (cioè con bit rate doppio rispetto alla banda del canale), ovviamente solo la prima armonica del segnale (quella con frequenza B) potrà passare attraverso il canale, mentre tutte le armoniche successive verranno più o meno attenuate (si riveda a questo proposito la discussione a proposito dell'ampiezza di banda di un segnale digitale).

In pratica il precedente criterio di Nyquist afferma che è sufficiente conservare la prima armonica sinusoidale di un segnale digitale affinché esso possa essere correttamente interpretato dal ricevitore:

In altre parole, se il canale si comporta da filtro passa-basso (ideale) e se tale filtro conserva almeno l'armonica fondamentale del segnale di partenza, il ricevitore può, usando uno squadratore (cioè un circuito che ricostruisca l'onda quadra in base al superamento o meno della soglia), rigenerare i livelli logici del segnale originale.

La formula precedente può anche essere considerata all'inverso, cioè se la banda disponibile del canale è minore di

B < velocità di trasmissione/2

non è possibile trasmettere correttamente sul canale evitando il problema dell'interferenza intersimbolica.

Occorre tuttavia sottolineare che il valore precedente va inteso come un limite massimo teorico, non raggiungibile nella pratica reale. Nella pratica si considera spesso un fattore di riduzione di circa 0,75 volte, rispetto al valore di C^binaria_max calcolato in base al teorema di Nyquist.

 

In realtà il precedente teorema di Nyquist esprime la capacità del canale non in bit al secondo, ma più in generale in simboli al secondo. Il simbolo è un concetto più astratto e generale rispetto al bit. Per esempio su un modem i simboli potrebbero corrispondere a diverse frequenze di tono o a diverse fasi del segnale sinusoidale trasmesso. Il teorema di Nyquist dunque stabilisce il massimo numero di simboli che può essere trasmesso su un canale.

C_max= 2 B

Considerando dunque un caso generale, la capacità del canale (espressa con la formula precedente) si misura in simboli al secondo ovvero in baud (unità di misura equivalente a simboli/s, detta anche baud rate, che prende il nome da Émile Baudot, inventore del codice Baudot utilizzato in telegrafia).

Possiamo dunque affermare in generale che il massimo baud rate tollerato da un mezzo di trasmissione è direttamente proporzionale alla banda del mezzo stesso e può essere stimato pari al doppio della banda stessa.

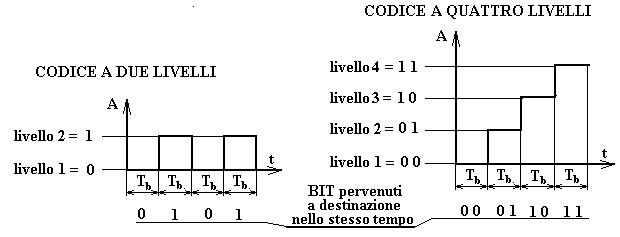
Se tale valore massimo non può essere aumentato (salvo cambiare il canale di trasmissione), tuttavia è possibile aumentare la velocità di trasmissione (espressa in bit al secondo) adottando una codifica multilivello, cioè usando più di due livelli logici per rappresentare i valori digitali. In generale se si usano M livelli il precedente teorema di Nyquist diventa:

C^multilivello_max = 2 B log₂(M)

Dove C^multilivello_max è la massima velocità di trasmissione espressa in bit al secondo usando una codifica multilivello. Per un sistema binario (a due livelli) M=2 e la formula si riduce alla precedente (il baud rate equivale ai bit al secondo).

Se si usa invece una codifica a 4 livelli, la capacità massima del canale (espressa in bps) raddoppia.

Si osservi che in base alla formula precedente aumentando il numero di livelli è possibile, in teoria, aumentare all'infinito la capacità del canale e dunque la velocità di trasmissione. Questo è vero solo in teoria se nel canale non è presente nessun rumore.

Di solito le codifiche multilivello non vengono effettuate in base all'ampiezza, ma facendo variare la fase di una portante sinusoidale (modulazioni digitali con portante sinusoidale): tuttavia la trattazione generale non cambia ed è più semplice, per comprendere i concetti, considerare una codifica effettuata in base all'ampiezza.

Aumentando il numero di livelli diminuisce la distanza fra un livello e l'altro, cioè diventa sempre più difficile distinguere fra loro i diversi livelli. Se nel canale è presente un rumore, all'aumentare del numero di livelli il rumore può facilmente diventare maggiore della "distanza" fra un livello e l'altro, compromettendo in tale modo la corretta interpretazione del segnale ricevuto.

Le precedenti formule di Nyquist valgono in teoria per un canale ideale, cioè assolutamente privo di rumore. Per un canale rumoroso la massima capacità teorica è data dal teorema di Shannon:

C^{canale_rumoroso}_max =  B log₂(1+S/N)

dove S/N è il rapporto segnale rumore presente sul canale stesso e C^{canale_rumoroso}_max si misura in bit/s.

Si noti che se N=0, cioè in assenza di rumore, la formula precedente fornisce C^{canale_rumoroso}_max  tendente all'infinito. Ciò non è assurdo, poiché, come si è già detto, in assenza di rumore sarebbe possibile in teoria adottare una codifica con un numero infinito di livelli e dunque trasmettere con una velocità (teorica) infinitamente elevata.

Facciamo un esempio pratico per comprendere meglio l'applicazione della teoria precedente. Supponiamo di considerare un canale telefonico con banda 300 a 3400 Hz. Considerando una codifica binaria (a due soli livelli) la massima velocità teorica che può essere raggiunta sul canale è data da:

C^binaria_max = 2 B = 2 x (3400-300) = 6200 b/s

Usando una codifica multilivello tale capacità può essere in teoria aumentata all'infinito, semplicemente aumentando il numero di livelli. Infatti:

C^multilivello_max = 2 B log₂(M) = 6200 x log₂(M)

Ciò però è possibile solo per un canale assolutamente privo di rumore. Supponiamo invece che sul nostro canale si abbia un rapporto segnale rumore SN = 36 dB. Abbiamo dunque 36dB = 10 log(S/N) da cui ricaviamo S/N = 10^36/10 = 3981.

Usando quindi  la formula di Shannon per canali rumorosi troviamo:

C^{canale_rumoroso}_max =  B log₂(1+S/N) = 3100 x log₂(1+3981) =

= 3100 x log₁₀(1+3981)/2 = 37073 bit/s.

Si tratta di una velocità di trasmissione molto maggiore di quella calcolata con la formula C^binaria_max (pari a soli 6200 bit/s). La differenza è dovuta al fatto che la formula di Shannon considera una codifica multilivello e non una semplice codifica binaria a due soli livelli.

Per sapere quanti livelli sarebbero in teoria necessari per raggiungere la velocità massima teorica di Shannon possiamo calcolare:

C^{canale_rumoroso}_max = C^multilivello_max

da cui

37073 bit/s = 2 B log₂(M) = 6200 log₂(M)

da cui

log₂(M) = 37073/6200 ≈ 6

In pratica occorrerebbe avere M≈64, cioè ben 64 livelli per raggiungere la velocità massima teorica prevista dalla formula di Shannon.

 

precedente - successiva

Sito realizzato in base al template offerto da

http://www.graphixmania.it

Segui @ElePrograMania